An Intuition for Long-Tailed Biological Variation
Long-tailed distributions are common in biology but less common in the way we think about biology or expect it to behave. A better intution for long tails can help us make better biological guesses and judgement calls.
Transcript
I'll start with today's central claim, which I hope can be a useful take-home message for people who want to build with biology: Biological change usually looks like multiplication rather than addition.
This is not a law of biology: biology doesn't really do laws. It's more like a rule of thumb. But I find it useful when I'm scoping out a new biological system and I wonder: how much can I change this system with engineering?
Let's do a concrete example. Let's say I'm a tomato breeder. I just crossed two varieties to make a new breed. So I grab some tomatoes and weigh them: one ounce and two ounces. How big do I expect the biggest tomatoes to be?
I'll make my guess by extrapolating from the little data that I have. If I assume that one and two ounce tomatoes are typical, I'd expect to see bigger tomatoes sometimes and much bigger tomatoes rarely.
But how should I extrapolate? Do I think that tomato variation looks like addition: 1, 2, 3, 4. Or do I think it looks like multiplication: 1, 2, 4, 8? If I'm dreaming of the world's biggest tomato (and I am, all the time) this choice determines how big I let myself dream.
There's no doubt that we're making extremely rough guesses here. If you happen to be an expert in tomato breeding, you can do better than this. But sometimes you need to make a quick judgment call, and when you do, biological change probably looks like multiplication.
In mathematical terms, we say that biological variation often follows a log-normal distribution. You're probably familiar with the normal distribution - it's the classic bell curve. Normal distributions are what tends to happen when you take a bunch of small random effects and add them up. Log-normal distributions are what tends to happen when you take a bunch of small random effects and multiply them.
One characteristic of a log-normal distribution is a long tail at the high end. When many small effects line up in the same direction, multiplication pushes them farther than addition would. Once you start seeing this in biological data, you can't unsee it. It shows up everywhere.
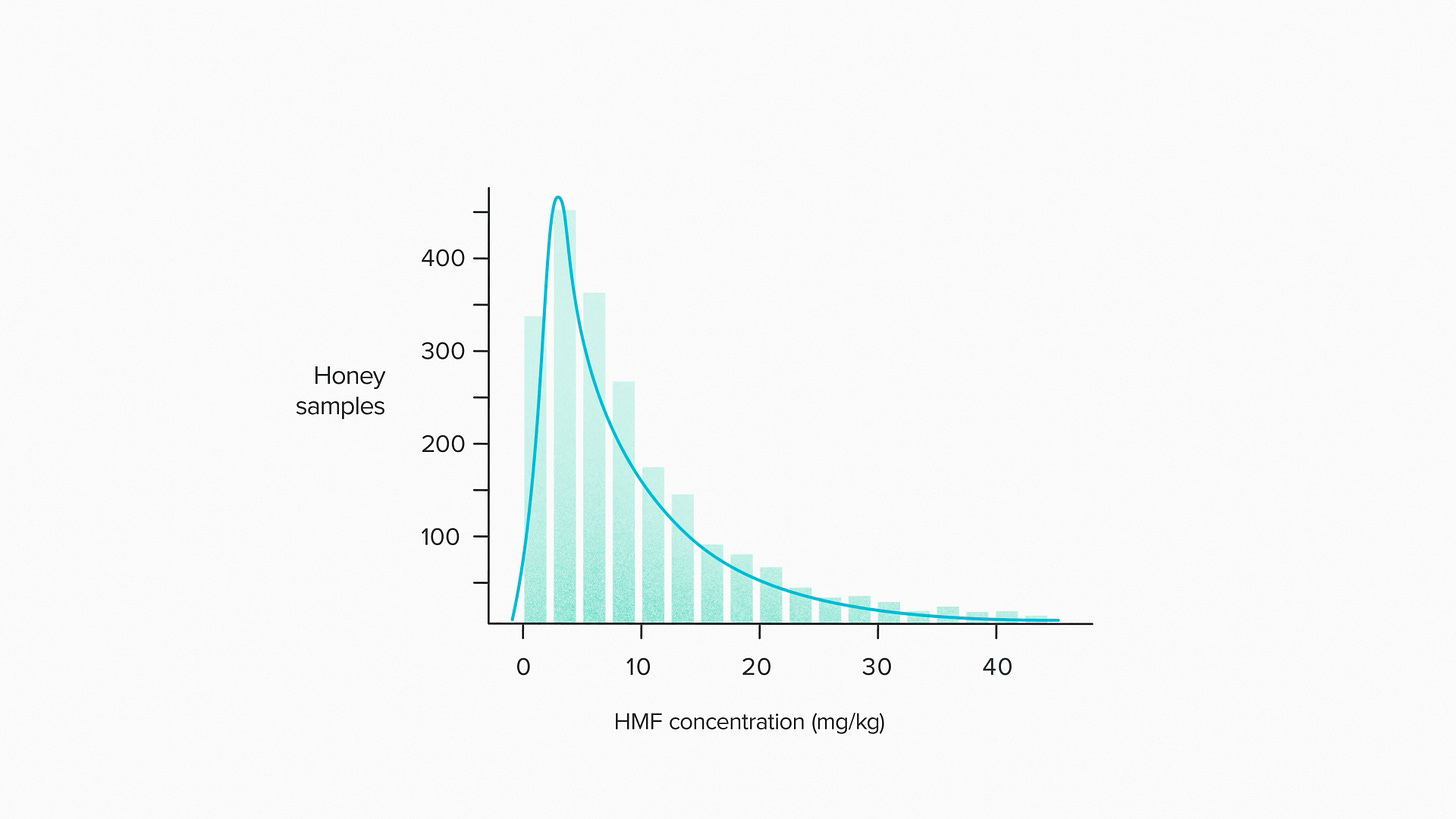
Take honey, for example. Honey naturally contains a molecule called hydroxymethylfurfural, or HMF, that is used as a marker for honey freshness. The concentration of HMF in honey follows a log-normal distribution: 10, 20, 40 (mg/kg)1. Why? I have no goddam idea. Except to say that is probably the result of many random effects that multiply.
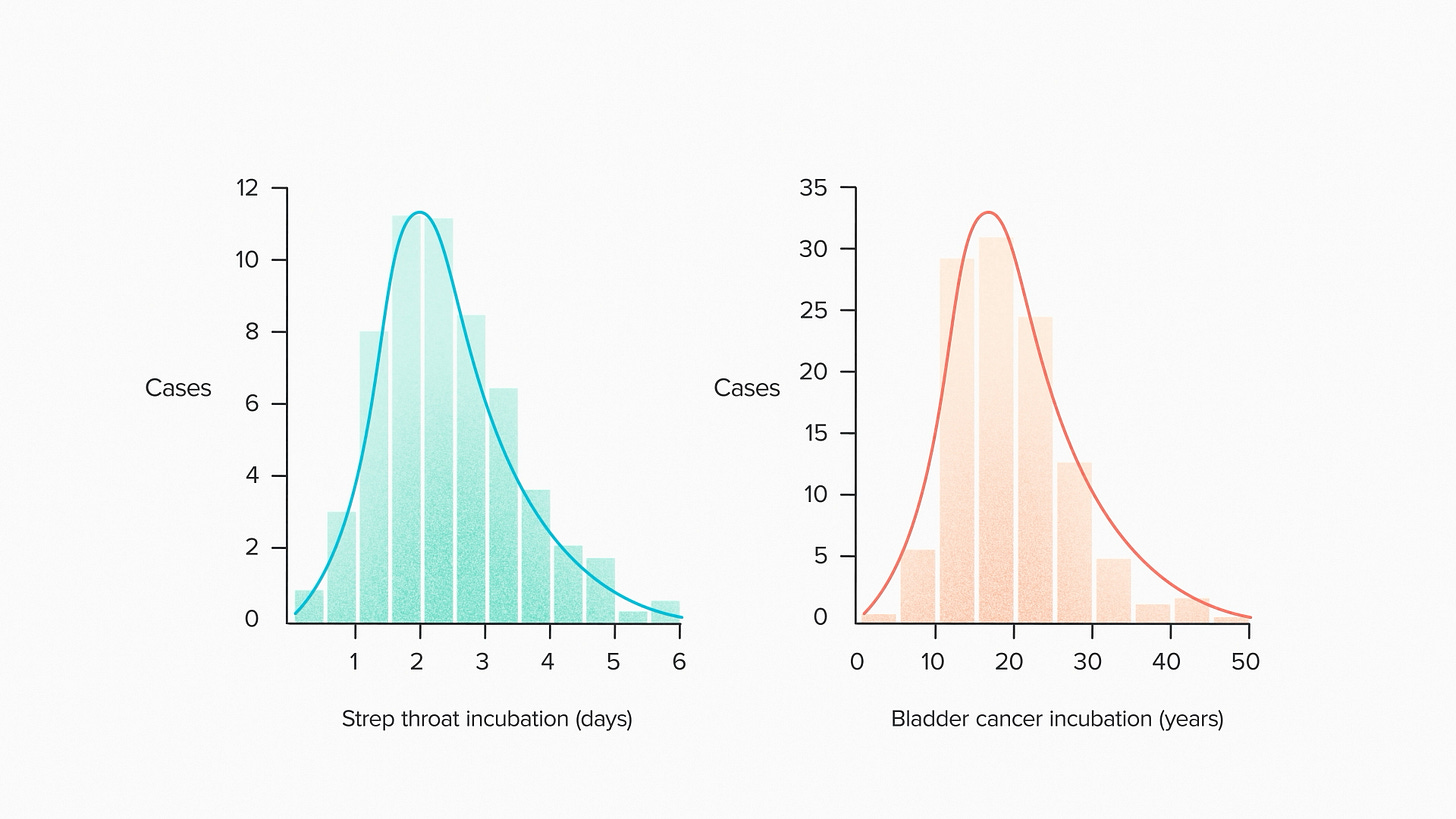
In the medical field, we see log-normal distributions in disease progression2. Here's the incubation time for strep throat, the number of days between exposure to a pathogen and the onset of symptoms. Here's the incubation time for bladder cancer, the number of years following exposure to a carcinogen. Two completely different diseases. Incubation in days or in years. But the same long tail.
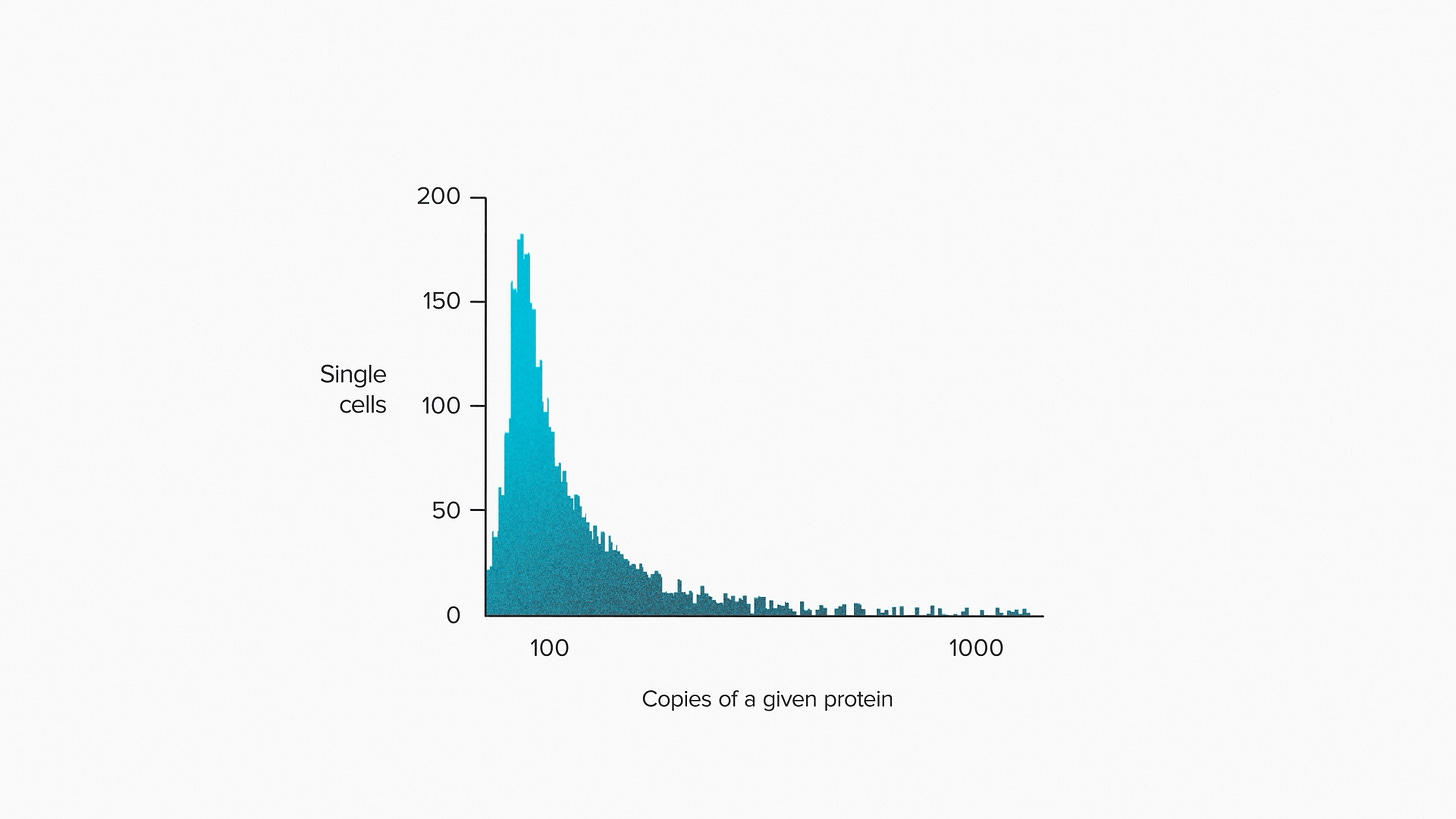
One more example. Let's zoom into a single bacterial cell and ask how many copies we can find of a particular protein3. Depending on the individual cell you're looking at, you might find 10, 100, 1000 or more floating around. If you're used to thinking of additive variation and normal distributions, that range might surprise you. These are the core functional components of a cell, and they're fluctuating by factors of 100? Madness! But once you've opened your eyes to the log normal in biology, it doesn't look strange at all.
Why does biological variation look like this? I can think of two reasons. The first is pretty simple: exponential growth. Every time a population of cells completes a cell cycle, it doubles: 2, 4, 8. So small changes in the generation time can result in exponential changes in the total number of cells.
The other reason has to do with the physics of binding. Most of what happens inside a cell is the result of proteins floating around and sticking to each other. Mutations to a protein sequence will change the free energy of binding, which roughly speaking has the effect of multiplying the number of proteins that end up bound. When you combine together many genetic changes, many multiplications, the result looks like a log normal distribution.
More or less. Most of the time. To all the biophysicists watching, I hope you can forgive me. I'm probably generalizing more than most scientists are comfortable with. But that's kind of the point. I'm not saying all biological variation is log normal - it isn't. I'm not saying every biological system can be improved by a factor of 1000 - it can't.
But what I am saying is that the log normal distribution is worth looking out for. Add the long tail to your mental model of biology and your intuitions will be a little better on average. Start with the expectation that biological change looks like multiplication, you'll be a step ahead most of the time.
Eckhard Limpert, Werner A. Stahel, Markus Abbt, Log-normal Distributions across the Sciences: Keys and Clues: On the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy way to characterize log-normal distributions, which can provide deeper insight into variability and probability—normal or log-normal: That is the question, BioScience, Volume 51, Issue 5, May 2001, Pages 341–352, https://doi.org/10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2
Bertrand Ottino-Loffler, Jacob G Scott, Steven H Strogatz (2017) Evolutionary dynamics of incubation periods eLife 6:e30212 https://doi.org/10.7554/eLife.30212
Furusawa C, Suzuki T, Kashiwagi A, Yomo T, Kaneko K. Ubiquity of log-normal distributions in intra-cellular reaction dynamics. Biophysics (Nagoya-shi). 2005 Apr 21;1:25-31. https://doi.org/10.2142/biophysics.1.25